How To Draw A Derivative
How To Draw A Derivative - Web the derivative f ′ (x) = 0 f ′ (x) = 0 when 1 − x 4 / 3 = 0. And our goal is to figure out which function is which. State the connection between derivatives and continuity. Describe three conditions for when a function does not have a derivative. This calculus video tutorial explains how to sketch the derivatives of the parent function using the graph f (x). The derivative of a function describes the function's instantaneous rate of change at a certain point. 👉 learn all about the applications of the derivative. Obtain a writing utensil and blank paper. Fill in this slope formula: Simplify it as best we can. If the derivative gives you a degree higher than 1, it is a curve. Graph a derivative function from the graph of a given function. Plot a function and its derivative, or graph the derivative directly. X2 + 2x δx + (δx)2 − x2 δx. Analyze a function and its derivatives to draw its graph. The graph of a derivative of a function f (x) is related to the graph of f (x). This relies on a solid understanding of functions, graphs, and the derivative as a function. Remember, this graph represents the derivative of a function. The derivative of a function describes the function's instantaneous rate of change at a certain point. X2 +. The graph of a derivative of a function f (x) is related to the graph of f (x). State the connection between derivatives and continuity. Remember, this graph represents the derivative of a function. Sketching the derivative of a function. Exercise \ (\pageindex {1}\) exercise \ (\pageindex {2}\) exercise \ (\pageindex {3}\) exercise \ (\pageindex {4}\) stage 2. Fill in this slope formula: Δy δx = f (x+δx) − f (x) δx. If the derivative (which lowers the degree of the starting function by 1) ends up with 1 or lower as the degree, it is linear. Web you just take the derivative of that function and plug the x coordinate of the given point into the derivative.. This relies on a solid understanding of functions, graphs, and the derivative as a function. Web about press copyright contact us creators advertise developers terms privacy policy & safety how youtube works test new features nfl sunday ticket press copyright. Which one is f, which is the first derivative, and which is the second? Expand (x+δx) 2 to x 2. Expand (x+δx) 2 to x 2 +2x δx+ (δx) 2: 1 − x 4 / 3 = 0. Where (f (x) has a tangent line with. Exercise \ (\pageindex {10}\) stage 1. Web courses on khan academy are always 100% free. Find space on a flat surface for you to work on. Another common interpretation is that the derivative gives us the slope of the line tangent to the function's graph at that point. The derivative of a function describes the function's instantaneous rate of change at a certain point. Then make δx shrink towards zero. Which one is f, which. Where (f (x) has a tangent line with. Our task is to find a possible graph of the function. Another common interpretation is that the derivative gives us the slope of the line tangent to the function's graph at that point. We'll explore how to use this powerful tool to determine the equation of the tangent line, enhancing our understanding. The graph of a derivative of a function f (x) is related to the graph of f (x). Web 732k views 7 years ago. And our goal is to figure out which function is which. Find space on a flat surface for you to work on. Web thanks to all of you who support me on patreon. Explore key concepts by building secant and tangent line sliders, or illustrate important calculus ideas like the mean value theorem. 1 − x 4 / 3 = 0. Examine an original graph that is on a coordinate plane of a function that you can differentiate (make a derivative of. Analyze a function and its derivatives to draw its graph. Here. Explore key concepts by building secant and tangent line sliders, or illustrate important calculus ideas like the mean value theorem. Which one is f, which is the first derivative, and which is the second? Mark zeros at the locations of any turning points or stationary inflection points. This video contains plenty of examples and practice. Exercise \ (\pageindex {5}\) exercise \ (\pageindex {6}\) exercise \ (\pageindex {7}\) exercise \ (\pageindex {8}\) exercise \ (\pageindex {9}\) stage 3. X = 0, x = 0, x = 1, x = 1, and x = −1. We'll explore how to use this powerful tool to determine the equation of the tangent line, enhancing our understanding of instantaneous rates of change. This is the graph of the function y = x. This calculus video tutorial explains how to sketch the derivatives of the parent function using the graph f (x). Where (f (x) has a tangent line with. First, we learn how to sketch the derivative graph of a continuous, differentiable function f (x), either given the original function or its graph y=f (x). The graph of a derivative of a function f (x) is related to the graph of f (x). Our task is to find a possible graph of the function. The derivative of a function describes the function's instantaneous rate of change at a certain point. Draw turning points at the location of any inflection points. F (x+δx) − f (x) δx.
Drawing the Graph of a Derivative YouTube

Steps to Sketch Graph of Function From Derivative YouTube

Draw the Function given Graph of Derivative YouTube

MATH221 Lesson 009B Drawing Derivatives YouTube
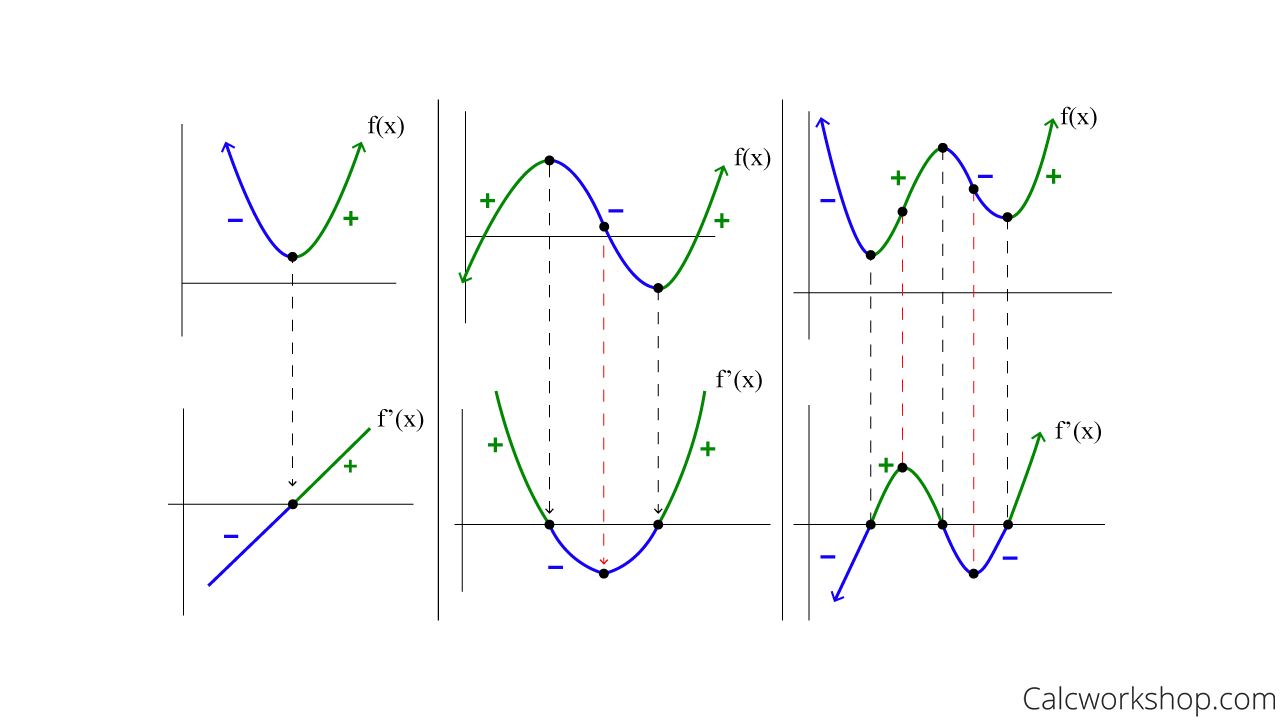
How To Sketch A Derivative Graph

How to sketch first derivative and Function from graph of second
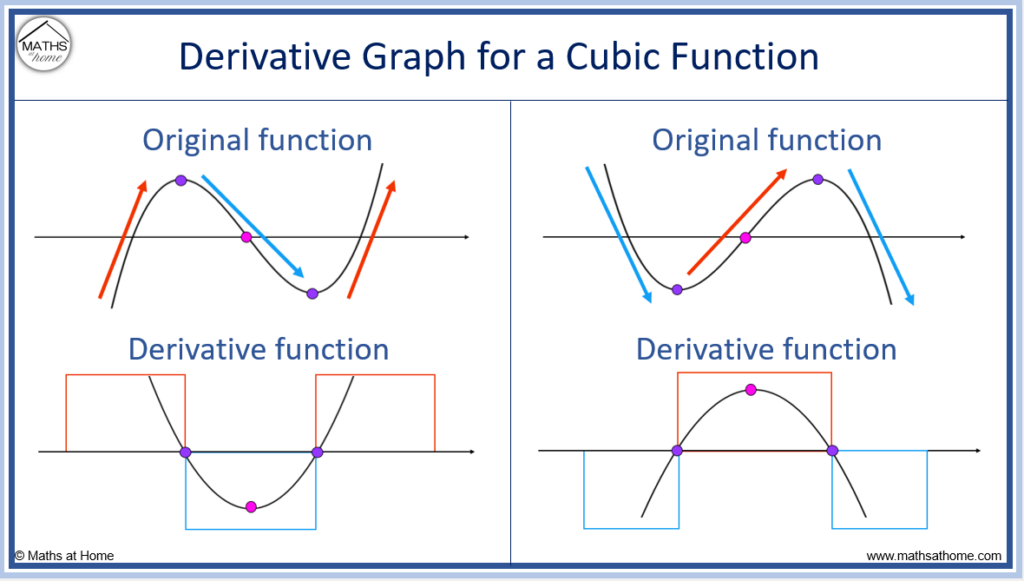
How to Sketch the Graph of the Derivative
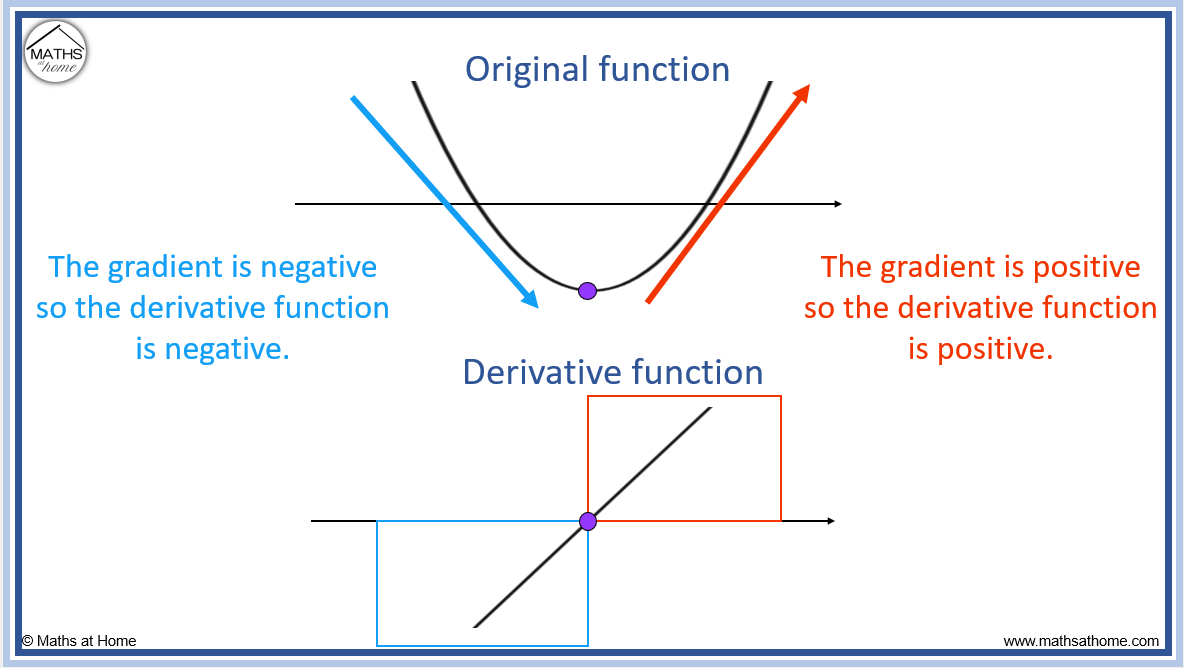
How to Sketch the Graph of the Derivative
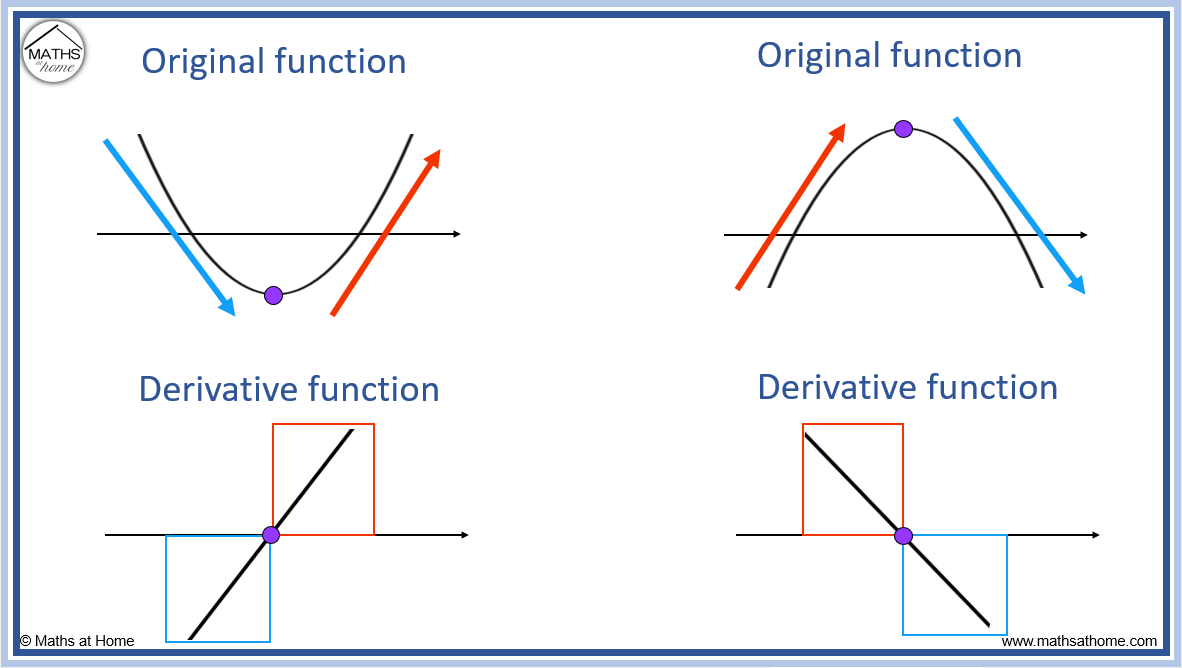
How to Sketch the Graph of the Derivative
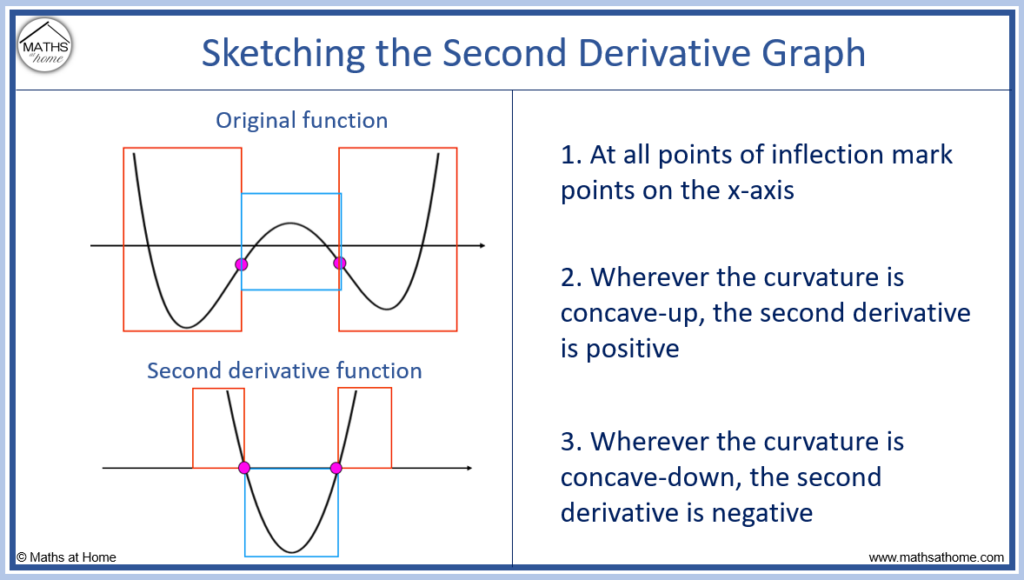
How to Sketch the Graph of the Derivative
Find Space On A Flat Surface For You To Work On.
If The Derivative Gives You A Degree Higher Than 1, It Is A Curve.
Let’s Start With An Easy One:
X2 + 2X Δx + (Δx)2 − X2 Δx.
Related Post: