How To Draw An Incenter
How To Draw An Incenter - This can be done by using a compass. We discuss these special points of concurrency in thi. One of several centers the triangle can have, the incenter is the point where the angle bisectors intersect. Web to construct the incenter, first construct the three angle bisectors; Web learn how to construct the incenter of a triangle in this free math video tutorial by mario's math tutoring using a compass and straightedge. We bisect the two angles using the method described in bisecting an angle. Place one of the compass's ends at one of the triangle's vertex. The steps to draw the angle bisectors are mentioned below: In this construction, we only use two, as this is sufficient to define the point where they intersect. Web now the above formula can be used: Web this page shows how to construct (draw) the incenter of a triangle with compass and straightedge or ruler. Scroll down the page for more examples and solutions on the incenters of triangles. 1.3k views 3 years ago. Web the following diagram shows the incenter of a triangle. Web to locate an incenter, you will need to draw a triangle. These midpoints will lie on the bisectors of the respective sides. This can be done by using a compass. Using angle bisectors to find the incenter and. Web learn how to construct the incenter of a triangle in this free math video tutorial by mario's math tutoring using a compass and straightedge. This construction is done by creating the angle. Construct an angle bisector for another angle of the triangle. The incenter of a triangle is the point where all three angle bisectors always intersect, and is the center of the triangle's. Scroll down the page for more examples and solutions on the incenters of triangles. Construct an angle bisector for one of the angles of the triangle. Web to. Web learn how to construct the incenter of a triangle in this free math video tutorial by mario's math tutoring using a compass and straightedge. Use this information to help you. The point where these three perpendicular bisectors intersect is the incenter of the triangle. Let’s understand this with the help of the below examples. 385 views 2 years ago. You can also drag the origin point at (0,0). I = \left (\dfrac {15 \cdot 0+13 \cdot 14+14 \cdot 5} {13+14+15}, \dfrac {15 \cdot 0+13 \cdot 0+14 \cdot 12} {13+14+15}\right)=\left (6, 4\right).\ _\square i = ( 13+ 14+1515 ⋅0+13⋅14 +14⋅5, 13+ 14+1515⋅ 0+13⋅0+ 14⋅12) = (6,4). However, in coordinate geometry, we can use the formula to get the incenter. Web. Web © 2024 google llc. Try this drag any point a,b,c. 1.3k views 3 years ago. In this construction, we only use two, as this is sufficient to define the point where they intersect. I = \left (\dfrac {15 \cdot 0+13 \cdot 14+14 \cdot 5} {13+14+15}, \dfrac {15 \cdot 0+13 \cdot 0+14 \cdot 12} {13+14+15}\right)=\left (6, 4\right).\ _\square i =. Web now the above formula can be used: Draw the perpendicular bisectors for the remaining sides of the triangle. These midpoints will lie on the bisectors of the respective sides. The incenter is always located within the triangle. In this construction, we only use two, as this is sufficient to define the point where they intersect. One of several centers the triangle can have, the incenter is the point where the angle bisectors intersect. Let’s understand this with the help of the below examples. In this construction, we only use two, as this is sufficient to define the point where they intersect. This geometry video tutorial explains how to identify the location of the incenter, circumcenter,. Try this drag any point a,b,c. This construction is done by creating the angle bisectors. This can be done by using a compass. The steps to draw the angle bisectors are mentioned below: The incenter o of the triangle abc is continuously recalculated using the above formula. This construction is done by creating the angle bisectors. Web in construction, we can find the incenter, by drawing the angle bisectors of the triangle. We discuss these special points of concurrency in thi. 385 views 2 years ago relationships within triangles. Draw the perpendicular bisectors for the remaining sides of the triangle. Web © 2024 google llc. Web the following diagram shows the incenter of a triangle. Using angle bisectors to find the incenter and. Find the coordinates of the incenter of a triangle whose vertices are given as a(20, 15), b(0, 0) and c. Scroll down the page for more examples and solutions on the incenters of triangles. Web learn what the incenter, circumcenter, centroid and orthocenter are in triangles and how to draw them. Web for a triangle, an incenter can be obtained by drawing the angle bisectors of the triangle and locate the point of intersection of these bisectors. I = \left (\dfrac {15 \cdot 0+13 \cdot 14+14 \cdot 5} {13+14+15}, \dfrac {15 \cdot 0+13 \cdot 0+14 \cdot 12} {13+14+15}\right)=\left (6, 4\right).\ _\square i = ( 13+ 14+1515 ⋅0+13⋅14 +14⋅5, 13+ 14+1515⋅ 0+13⋅0+ 14⋅12) = (6,4). The steps to draw the angle bisectors are mentioned below: You can also drag the origin point at (0,0). To locate the incenter, one can draw each of the three angle bisectors, and then determine the point at which they all intersect. This can be done by using a compass. We bisect the two angles using the method described in bisecting an angle. Incenter = (side a + side b + side c) / 3 Web now the above formula can be used: With three angle bisectors, you construct an incenter.
how to draw a incenter YouTube

How to draw an incenter on geogebra YouTube
Incenter, Circumcenter and Centroid How to easily find these points
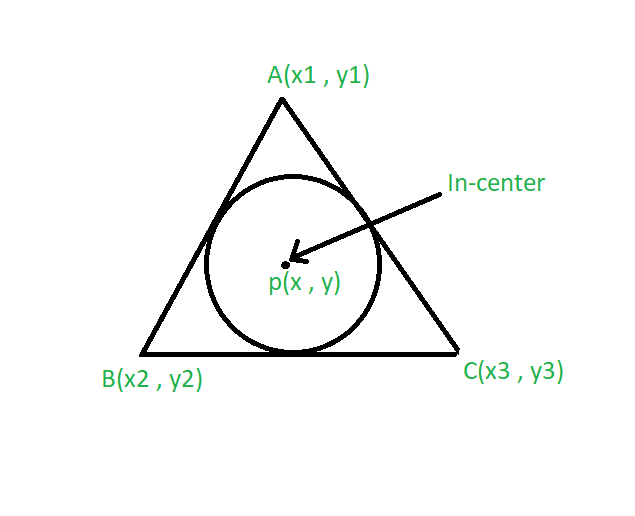
How To Find Incenter Of A Triangle With Coordinates We start with the

How to draw the Incenter and the Inscribed Circle of a triangle YouTube

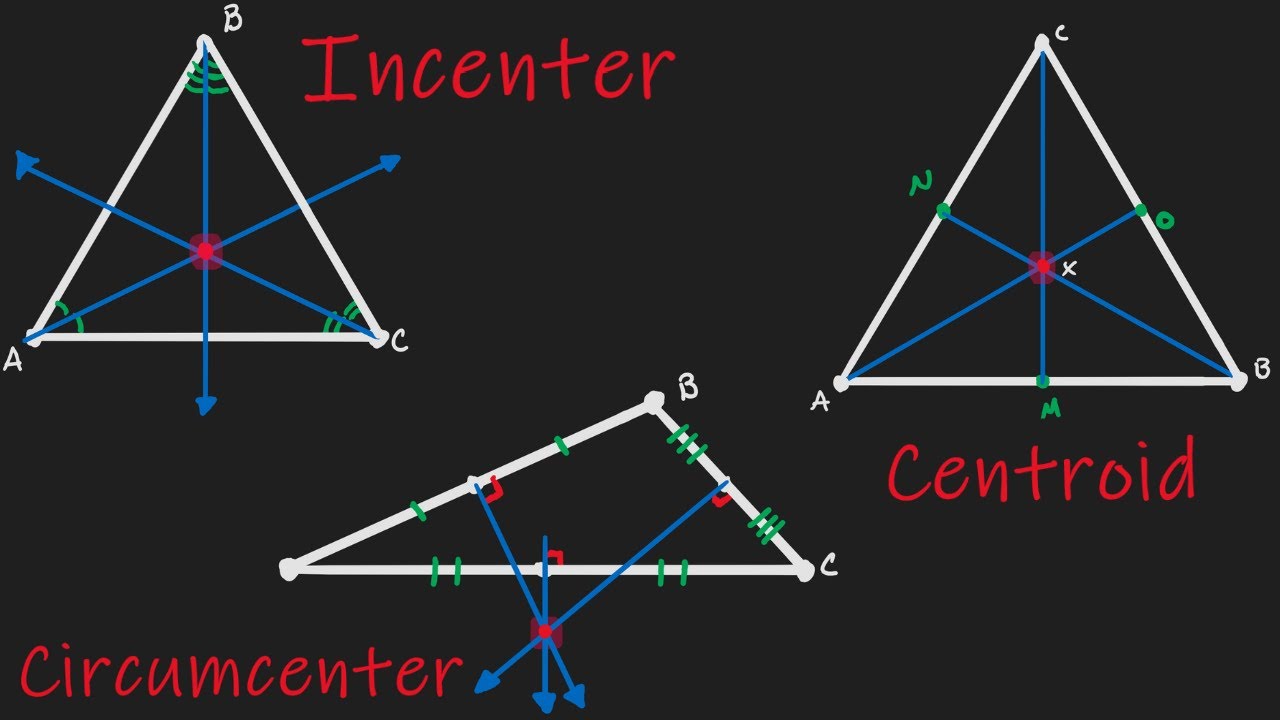
Incenter, Circumcenter, Orthocenter & Centroid of a Triangle Geometry

Incenter of a triangle Definition, Properties and Examples Cuemath
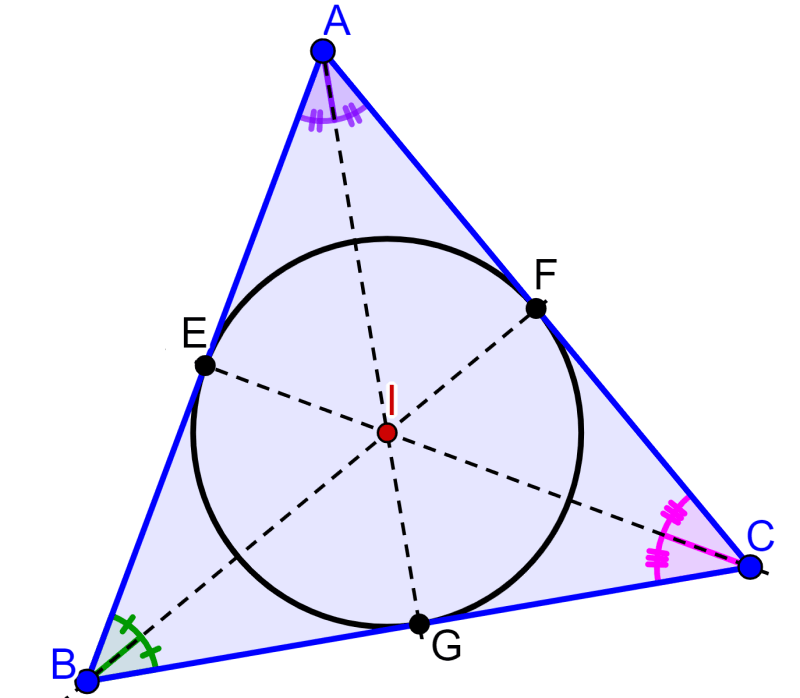
How to find the incenter of a triangle? Step by step Neurochispas

Incenter of a triangle Definition, Properties and Examples Cuemath

Incenter of a triangle Definition, Properties and Examples Cuemath
Let’s Understand This With The Help Of The Below Examples.
164K Views 12 Years Ago Special Properties And Parts Of Triangles | Geometry | Khan Academy.
These Midpoints Will Lie On The Bisectors Of The Respective Sides.
Web Incenter (I) Of A Triangle = (Ax 1 + Bx 2 + Cx 3 /A + B + C, Ay 1 + By 2 + Cy 3 /A + B + C), Here Vertices A = (0, 0), B = (14, 0), And C = (5, 12)And Side Lengths Bc = 15, Ac = 13, & Ab = 14 I = (15 × 0 + 13 × 14 + 14 × 5/13 + 14 +.
Related Post: